Som transmissionsmekanism används planetväxlar i stor utsträckning inom olika tekniska tillämpningar, såsom reducerväxlar, kranväxlar, planetväxlar etc. För planetväxlar kan den i många fall ersätta transmissionsmekanismen för en fastaxelväxel. Eftersom kugghjulsöverföringen är i linjekontakt, kommer långvarig ingrepp att orsaka kugghjulsfel, så det är nödvändigt att simulera dess hållfasthet. Li Hongli et al. använde den automatiska ingreppsmetoden för att gripa in i planetväxeln och erhöll att vridmomentet och den maximala spänningen är linjära. Wang Yanjun et al. satte också planetväxeln i ingrepp genom den automatiska genereringsmetoden och simulerade statik och modal simulering av planetväxeln. I denna artikel används tetraeder- och hexaederelement huvudsakligen för att dela upp nätet, och de slutliga resultaten analyseras för att se om hållfasthetsvillkoren är uppfyllda.

1. Modellupprättande och resultatanalys

Tredimensionell modellering av planetväxel

Planetväxelbestår huvudsakligen av ringhjul, solhjul och planethjul. De viktigaste parametrarna som valts i denna artikel är: antalet tänder på den inre kuggkransen är 66, antalet tänder på solhjulet är 36, antalet tänder på planethjulet är 15, den yttre diametern på den inre kuggkransen är 150 mm, modulen är 2 mm, tryckvinkeln är 20 °, tandbredden är 20 mm, tilläggshöjdkoefficienten är 1, glappkoefficienten är 0,25 och det finns tre planethjul.

Statisk simuleringsanalys av planetväxel

Definiera materialegenskaper: importera det tredimensionella planetväxelsystemet som ritats i UG-programvaran till ANSYS och ställ in materialparametrarna enligt tabell 1 nedan:

Nätverk: Det finita elementnätet delas in i tetraeder och hexaeder, och elementets grundstorlek är 5 mm. Eftersomplanetväxel, solhjulet och den inre kuggringen är i kontakt och ingriper, nätet mellan kontakt- och nätdelarna är förtätat och storleken är 2 mm. Först används tetraedriska rutnät, som visas i figur 1. Totalt 105906 element och 177893 noder genereras. Sedan används ett hexaedriskt rutnät, som visas i figur 2, och totalt 26957 celler och 140560 noder genereras.

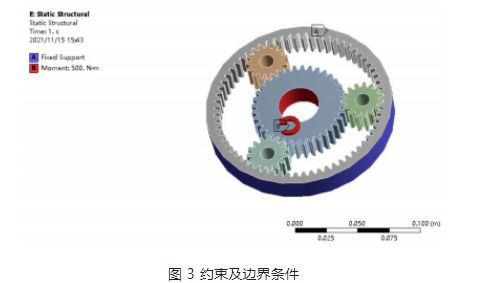
Lastapplikation och randvillkor: enligt planetväxelns arbetsegenskaper i reducerväxeln är solväxeln drivväxeln, planetväxeln är den drivna växeln och den slutliga utmatningen sker genom planetbäraren. Fäst den inre kuggkransen i ANSYS och applicera ett vridmoment på 500 N·m på solväxeln, som visas i figur 3.

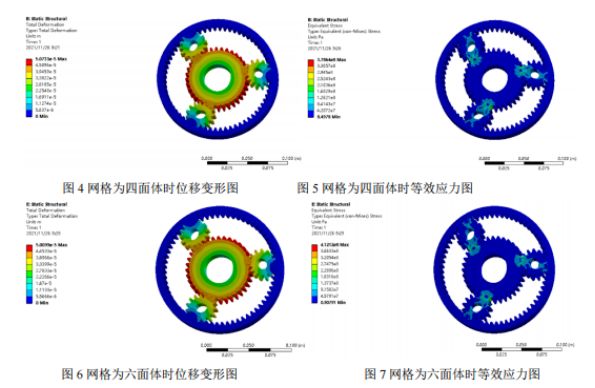
Efterbehandling och resultatanalys: Förskjutningsnefhogrammet och ekvivalent spänningsnefhogrammet från statisk analys erhållna från två rutnätsindelningar ges nedan, och jämförande analys utförs. Från förskjutningsnefhogrammet för de två typerna av rutnät konstateras att den maximala förskjutningen sker vid den position där solhjulet inte griper in i planethjulet, och den maximala spänningen sker vid roten av kugghjulsingreppet. Den maximala spänningen i det tetraedriska rutnätet är 378 MPa, och den maximala spänningen i det hexaedriska rutnätet är 412 MPa. Eftersom materialets sträckgräns är 785 MPa och säkerhetsfaktorn är 1,5, är den tillåtna spänningen 523 MPa. Den maximala spänningen för båda resultaten är mindre än den tillåtna spänningen, och båda uppfyller hållfasthetsvillkoren.

2. Slutsats

Genom finita elementsimuleringen av planetväxeln erhålls förskjutningsdeformationsnephogrammet och ekvivalent spänningsnephogrammet för växelsystemet, från vilket maximi- och minimidata och deras fördelning iplanetväxelmodellen kan hittas. Platsen för den maximala ekvivalenta spänningen är också den plats där kuggarna är mest benägna att gå sönder, så särskild uppmärksamhet bör ägnas åt den under konstruktion eller tillverkning. Genom analys av hela planetväxelsystemet elimineras felet som orsakas av analysen av endast en kuggtand.