Vad används epicykliska kugghjul till?

Epicykliska kugghjuläven kända som planetväxelsystem, används ofta inom olika branscher tack vare sin kompakta design, höga effektivitet och mångsidighet.

Dessa kugghjul används främst i applikationer där utrymmet är begränsat, men högt vridmoment och hastighetsvariation är avgörande.

1. Bilväxellådor: Epicykliska kugghjul är en nyckelkomponent i automatväxellådor och ger sömlösa växlingar, högt vridmoment vid låga hastigheter och effektiv kraftöverföring.
2. Industrimaskiner: De används i tunga maskiner för sin förmåga att hantera höga belastningar, fördela vridmomentet jämnt och arbeta effektivt i kompakta utrymmen.
3. Flyg- och rymdteknik: Dessa kugghjul spelar en avgörande roll i flygmotorer och helikoptrar och säkerställer tillförlitlighet och exakt rörelsekontroll under krävande förhållanden.
4. Robotik och automation: Inom robotik används epicykliska kugghjul för att uppnå exakt rörelsekontroll, kompakt design och högt vridmoment i begränsade utrymmen.

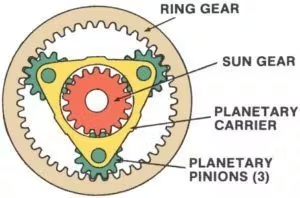
Vilka är de fyra elementen i den epicykliska växeln?

En epicyklisk kugghjulsuppsättning, även känd som enplanetväxel system, är en mycket effektiv och kompakt mekanism som vanligtvis används i fordonsväxellådor, robotteknik och industrimaskiner. Detta system består av fyra huvudelement:

1. SolutrustningSolhjulet, som är placerat i mitten av kugghjulet, är den primära drivkraften eller mottagaren av rörelse. Det samverkar direkt med planethjulen och fungerar ofta som systemets ingång eller utgång.

2. PlanetväxlarDet här är flera kugghjul som roterar runt solhjulet. De är monterade på en planethjulshållare och griper in i både solhjulet och ringhjulet. Planethjulen fördelar lasten jämnt, vilket gör att systemet kan hantera högt vridmoment.

3.PlanetbärareDenna komponent håller planethjulen på plats och stöder deras rotation runt solhjulet. Planethållaren kan fungera som ett ingångs-, utgångs- eller stationärt element beroende på systemets konfiguration.

4.RingdrevDetta är ett stort yttre kugghjul som omger planetdreven. Ringdrevets inre kuggar griper in i planetdreven. Liksom de andra elementen kan ringdrevet fungera som ingång, utgång eller förbli stationärt.

Samspelet mellan dessa fyra element ger flexibiliteten att uppnå olika hastighetsförhållanden och riktningsförändringar inom en kompakt struktur.

Hur man beräknar utväxlingsförhållandet i en epicyklisk kugghjulsuppsättning?

Utväxlingsförhållandet för enepicyklisk kugghjulssats beror på vilka komponenter som är fasta, ingång och utgång. Här är en steg-för-steg-guide för att beräkna utväxlingsförhållandet:

1. Förstå systemkonfigurationen:

Identifiera vilket element (solen, planetbäraren eller ringen) som är stationärt.

Bestäm ingångs- och utgångskomponenterna.

2. Använd den grundläggande utväxlingsekvationen: Utväxlingsförhållandet för ett epicykliskt kugghjulssystem kan beräknas med hjälp av:

GR = 1 + (R / S)

Där:

GR = Utväxlingsförhållande

R = Antal kuggar på ringdrevet

S = Antal tänder på solhjulet

Denna ekvation gäller när planetbäraren är utgången, och antingen solen eller ringhjulet är stillastående.

3. Justera för andra konfigurationer:

• Om solhjulet är stillastående påverkas systemets utgående hastighet av förhållandet mellan ringhjulet och planethjulet.
• Om ringhjulet är stillastående bestäms utgångsvarvtalet av förhållandet mellan solhjulet och planetbäraren.

4. Backväxelförhållande för utgång till ingång: Vid beräkning av hastighetsreduktion (ingång högre än utgång) är förhållandet enkelt. För hastighetsmultiplikation (utgång högre än ingång), invertera det beräknade förhållandet.

Exempelberäkning:

Anta att en kugghjulsuppsättning har:

Ringdrev (R): 72 tänder

Soldrev (S): 24 tänder

Om planetbäraren är utgången och solhjulet är stillastående, är utväxlingsförhållandet:

GR = 1 + (72 / 24) GR = 1 + 3 = 4

Detta innebär att utgångshastigheten blir fyra gånger långsammare än ingångshastigheten, vilket ger ett reduktionsförhållande på 4:1.

Att förstå dessa principer gör det möjligt för ingenjörer att designa effektiva och mångsidiga system skräddarsydda för specifika tillämpningar.